基于Newton_Raphson算法的除法器实现网站首页 学无止境

基于Newton_Raphson算法的除法器实现

李逍遥lzx 2025-07-30 00:01:04

简介基于Newton_Raphson算法的除法器实现

https://blog.csdn.net/qq_38360574/article/details/145299223?spm=1001.2014.3001.5501

上文的除法器实现思路由除法的运算过程得出，而牛顿迭代法实现除法器则将除法转换为方程根的求解。本文将按照下述的顺序进行：1.简要介绍牛顿迭代法 2.牛顿迭代法实现除法器的思路 3.使用matlab对基于牛顿迭代法的除法器进行仿真 4.verilog实现除法器

1.牛顿迭代法

牛顿迭代法是一种用于求解非线性方程的数值方法。它通过迭代逼近方程的根，具有快速收敛的特点，广泛应用于科学计算、工程优化和硬件设计中。

1.1基本思想

牛顿迭代法的核心思想是利用函数的泰勒展开，通过线性近似逐步逼近方程的根。具体步骤如下：

a. 初始猜测：选择一个初始猜测值，记为 $x_{n}$

b. 迭代公式：根据当前猜测值计算下一个猜测值： $x_{n+1}$

$x_{n+1} = x_{n}-f(x_{n})_/{f^{'}(x_{n}))}$

1.2 几何解释

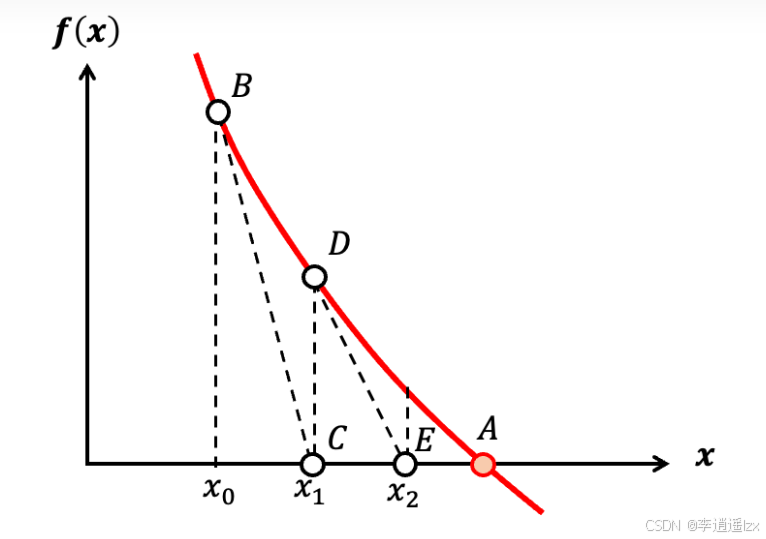
牛顿迭代法的本质是在每一次迭代中用函数的切线近似代替曲线，并将切线与x轴的交点作为下一个猜测值

切线方程：

$y=f(x_{n})+f^{'}(x_{n}))(x-x_{n})$

令 $f(x_{n})=0$ , 解得 :

$x_{n+1}=x_{n}-f(x_{n})/f^{'}(x_{n}))$

2.牛顿迭代法实现除法器的思路

$f(x) = 1/x - D = 0$

令D = divisor 则 x = 1/divisor, 因此求取1/divisor便转换为f(x) = 0的根的求解

$f^{'}(x)=-(frac{1}{x})^2$

$f^{'}(x_{n})=-(frac{1}{x_{n}})^2$

有：

$x_{n+1}=x_{n}(2-Dx_{n})$ 。

问题转换为上式的递归

3.matlab仿真

dividend = 240; %除数
divisor = 12;   %被除数
QUOTIENT=0

x1=1;
cnt_a = 1;      %计数器
D = 12/2^8;
buffer1= zeros(100,1);
buffer2= zeros(100,1);
buffer3= zeros(100,1);
buffer4= zeros(100,1);
buffer5= zeros(100,1);
buffer5= zeros(100,6);

while(cnt_a ~= 100)
    x2=x1*(2-D*x1);             %迭代
    x1 = floor(x2*256)/256;     %定点化处理
    QUOTIENT = x1/2^8*dividend; %商
    buffer1(cnt_a) = x1;
    buffer2(cnt_a) = D*x1;
    buffer3(cnt_a )= 2-D*x1;
    buffer4(cnt_a) = x2 ;
    buffer5(cnt_a) = QUOTIENT;
    buffer6 = [buffer1(:,1) , buffer2(:,1), buffer3(:,1) , buffer4(:,1),buffer5(:,1)];
    cnt_a = cnt_a + 1;  
end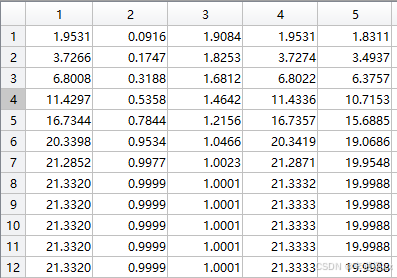

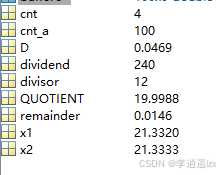
第10次迭代后输出稳定值

4.verilog实现除法器

本次实现将除数与被除数的位宽定义为8位。端口声明如下：

module Divisor_newton(
    input                               sys_clk         ,
    input                               rst             ,
    input  [7 : 0]                      dividend        ,
    input  [7 : 0]                      divisor         ,
    input                               divide_in_vld   ,
    output reg [7 : 0]                  quotient        ,
    output reg [7 : 0]                  remainder       ,
    output reg                          divide_out_vld          
);

所要计算的公式为：

$x_{n+1}=x_{n}(2-Dx_{n})$

xn的初始值为1，D<=1, D其实就是divisor，我们端口定义中的divisor位宽为8 ，如果将x[7]视为小数点后第一位，则D = divisor/2^8 ,1={1'b1,8'd0 }, 2={2'd2,8'd0}。从上式计算得到的结果为1/divisor*2^8。

声明以下寄存器 ,含义及位宽如下

Xn : 迭代变量，位宽为16，小数部分8位

DXn : D*Xn , 位宽为24，小数部分16位

data_2_DXn : 2 - DXn，位宽24，小数部分16位

Xn_x_data_2_DXn : xn*(2-DXn)，位宽40，小数部分24位。

因为是迭代公式，意味将计算得到的结果又代入到变量当中，那么便有一个问题，何时结束运算，因为从上文matlab的仿真可以看出，如果能够收敛，那么当变量的值出现重复之后，变量的值就不会再发生变化了，因此本文将连续三个变量结果相等作为结束的条件，并以此作为触发条件，计算余数。

`timescale 1ns / 1ps

module Divisor_newton(
    input                               sys_clk         ,
    input                               rst             ,
    input  [7 : 0]                      dividend        ,
    input  [7 : 0]                      divisor         ,
    input                               divide_in_vld   ,
    output reg [7 : 0]                  quotient        ,
    output reg [7 : 0]                  remainder       ,
    output reg                          divide_out_vld          
);
//-------------------------------------------------------- 
reg  [15:0]         Xn; 
wire [23:0]         DXn;
reg  [23:0]         data_2_DXn;
reg                 divide_in_vld_r1;
reg                 divide_in_vld_r2;
reg                 divide_in_vld_r3;
reg                 divide_in_vld_r4;
reg                 divide_in_vld_r5;
reg                 divide_in_vld_r6;
reg                 divide_in_vld_r7;
wire [39:0]         Xn_x_data_2_DXn;
wire [23:0]         Xn_x_dividend;

//-----------------
//打拍

    always@(posedge sys_clk)begin
        if(rst||divide_out_vld)begin
            divide_in_vld_r1 <= 'd0;
            divide_in_vld_r2 <= 'd0;
            divide_in_vld_r3 <= 'd0;
            divide_in_vld_r4 <= 'd0;    
            divide_in_vld_r5 <= 'd0;
            divide_in_vld_r6 <= 'd0;
        end
        else begin
         divide_in_vld_r1 <= divide_in_vld|divide_in_vld_r4    ;
         divide_in_vld_r2 <= divide_in_vld_r1;
         divide_in_vld_r3 <= divide_in_vld_r2   ;
         divide_in_vld_r4 <= divide_in_vld_r3   ;
         divide_in_vld_r5 <= divide_in_vld_r4   ;
         divide_in_vld_r6 <= divide_in_vld_r5   ;
         divide_in_vld_r7 <= divide_in_vld_r6   ;
    end
end

//-------------------
//迭代计算

    always@(posedge sys_clk)begin                  //整数和小数部分各8位
        if(rst)
            Xn <= 'd0;
        else if(divide_in_vld)
            Xn <= {8'd1,8'd0};
        else if(divide_in_vld_r4)
            Xn <= Xn_x_data_2_DXn[31:16];      
    end

mult_D_Xn u_mult_D_Xn (                                         
                          .CLK  (sys_clk    ),  // input wire CLK
                          .A    (divisor    ),      // input wire [7 : 0] A
                          .B    (Xn         ),      // input wire [15 : 0] B
                          .P    (DXn        )      // output wire [23 : 0] P
                        );

always@(posedge sys_clk)begin          //小数部分16位                         
    if(rst)
        data_2_DXn <= 'd0;
    else if(divide_in_vld_r2)
        data_2_DXn <= {8'd2,16'd0} - DXn;
end

mult_xn_x_2_Dxn u_mult_xn_x_2_Dxn (                             
                                      .CLK  (sys_clk            ),  // input wire CLK
                                      .A    (Xn                 ),      // input wire [15 : 0] A
                                      .B    (data_2_DXn         ),      // input wire [23 : 0] B
                                      .P    (Xn_x_data_2_DXn    )      // output wire [26 : 0] P
                                    );

mult_Xn_x_dividend u_mult_Xn_x_dividend (
                                          .CLK  (sys_clk        ),  // input wire CLK
                                          .A    (Xn             ),      // input wire [8 : 0] A
                                          .B    (dividend       ),      // input wire [7 : 0] B
                                          .P    (Xn_x_dividend  )      // output wire [16 : 0] P
                                        );

always@(posedge sys_clk)begin   
    if(rst)
        quotient <= 'd0;
    else if(divide_in_vld_r4)
        quotient <= Xn_x_dividend[15]? Xn_x_dividend[23:16] + 1 : Xn_x_dividend[23:16];
end

//------------------
//余数计算

wire [15:0] divisor_x_quotient;

mult_divisor_x_quotient u_mult_divisor_x_quotient (     
  .CLK(sys_clk),  // input wire CLK
  .A(quotient),      // input wire [7 : 0] A
  .B(divisor),      // input wire [7 : 0] B
  .P(divisor_x_quotient)      // output wire [15 : 0] P
);

    always@(posedge sys_clk)begin
        if(rst)
            remainder <= 'd0;
        else if(divide_in_vld_r6) 
            remainder <= dividend - divisor_x_quotient[7:0];
    end

//------------------------
//检验是否结束迭代
reg [7:0]  quotient_r1   ;
reg [7:0]  quotient_r2  ;

always@(posedge sys_clk)begin
    if(rst)begin
        quotient_r1  <= 'd0;
        quotient_r2 <= 'd0;    
    end 
    else if(divide_in_vld_r5)begin
        quotient_r1  <= quotient;
        quotient_r2 <= quotient_r1;
    end     
end

always@(posedge sys_clk)begin
    if(rst)
        divide_out_vld <= 'd0;     
    else if(divide_in_vld_r7 && quotient == quotient_r1 && quotient == quotient_r2 )
        divide_out_vld <= 'd1;
    else if(divide_out_vld)
        divide_out_vld <= 'd0;
end

endmodule

仿真