您现在的位置是：首页 >学无止境 >那几个排序算法你搞懂了吗？快进来看看吧！！（Python & C/C++）网站首页学无止境
那几个排序算法你搞懂了吗？快进来看看吧！！（Python & C/C++）
简介那几个排序算法你搞懂了吗？快进来看看吧！！（Python & C/C++）
早上好啊，大佬们，这个付费专栏不一般呐，绝对物超所值。
咱们的第一篇要说什么涅？没错了，排序算法，经典，好吧！
啥子是排序算法噻
说白了，排序算法就是把那堆乱七八糟的数据，按照一定规则给它整得明明白白、规规矩矩的。就好比你桌上一堆乱放的扑克牌，排序后就按大小顺序排得整整齐齐。举个例子，有这么一组数字 [5, 3, 1, 4, 2] ，经过排序，它就变成了 [1, 2, 3, 4, 5]，这就是排序算法干的事儿，简单吧！
1. 冒泡排序（跟喝醉的胖子一样晃悠）
这货就像醉汉在酒吧找厕所，走一步晃三下，见到不顺眼的就换位置！
思路
（1）最后一间小隔间的醉汉不想呆在自己那儿，他晃晃悠悠地跑出去和隔壁小隔间的醉汉比酒劲。要是他觉得自己比隔壁的厉害，就和隔壁的换个小隔间。
（2）要是他发现自己比隔壁的弱，那就不换了。接着，隔壁的醉汉也会从自己小隔间出来，和同方向下一个小隔间的醉汉比酒劲，就这么一个接一个地比下去，没完没了地重复这个过程。
（3）等每个醉汉都找到自己满意的小隔间（就像找到自己喜欢的厕所一样），就不会再换了。
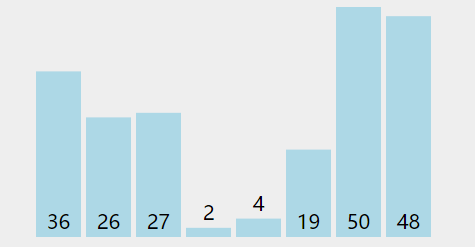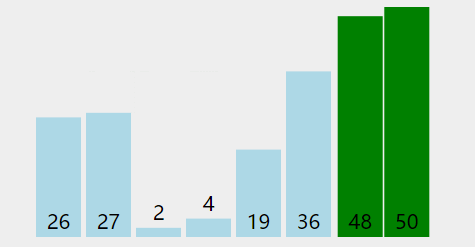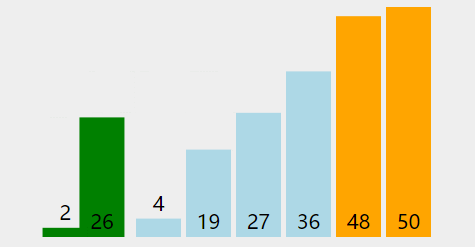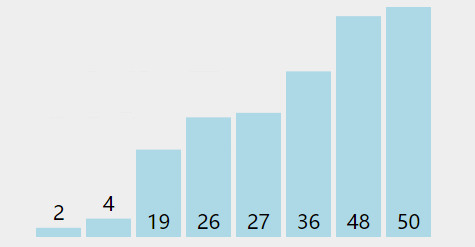
C++版：
#include <bits/stdc++.h>
using namespace std;
void bubbleSort(int arr[], int n) {
for(int i=0; i<n-1; ++i) { // 跟特么遛狗一样来回溜达
for(int j=0; j<n-i-1; ++j) { // 每次少溜达一圈
if(arr[j] > arr[j+1]) { // 看隔壁不顺眼就干架
swap(arr[j], arr[j+1]); // 干不过就换位置
}
}
}
}
int main()
{
int arr[10] = {5, 2, 3, 1, 7, 4, 9, 0, 8, 6};
bubbleSort(arr, 10);
for(int i:arr) cout << i << " ";
//0 1 2 3 4 5 6 7 8 9
return 0;
}
Python版：
def bubble_sort(arr):
n = len(arr)
for i in range(n-1): # 总共要溜达n-1趟
for j in range(n-i-1): # 每次少管一个闲事
if arr[j] > arr[j+1]: # 瞅见大的就怼
arr[j], arr[j+1] = arr[j+1], arr[j] # 直接换座儿
arr = [5, 2, 3, 1, 7, 4, 9, 0, 8, 6]
bubble_sort(arr)
print(arr)
#[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
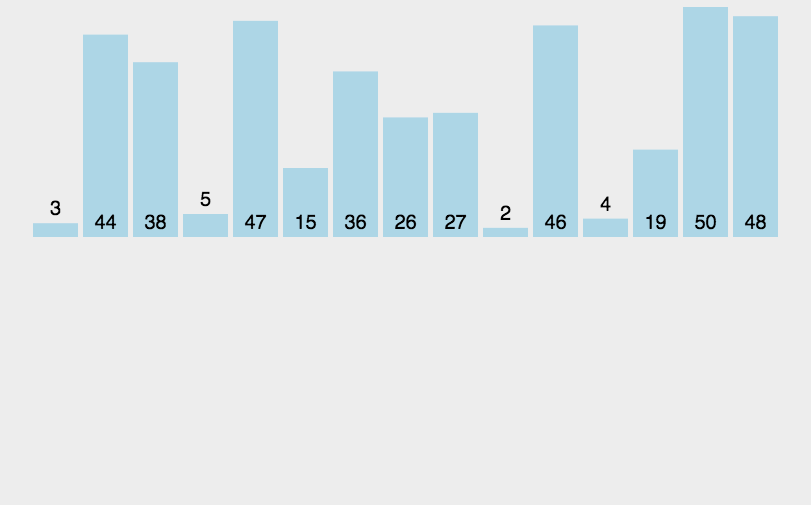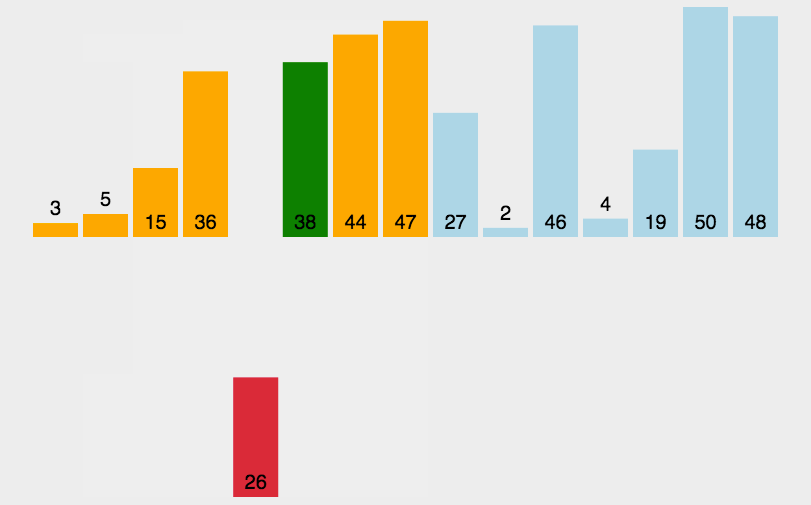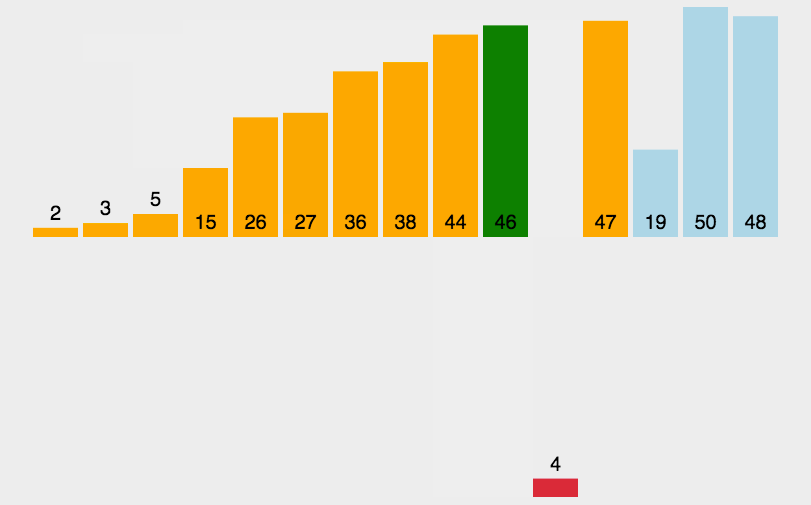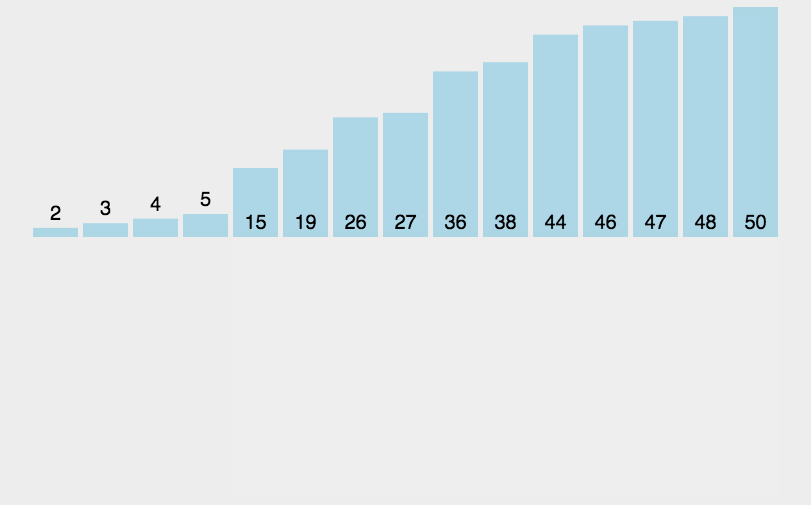
2. 选择排序（跟菜市场挑菜似的）
这货跟大妈买菜一样，每次都要挑最新鲜的萝卜！
思路
（1）每次挑出一根最好的萝卜，放到最边上。
（2）在剩下的萝卜里再挑出最好的。
（3）循环上面的操作。
C++版：
#include <bits/stdc++.h>
using namespace std;
void selectionSort(int arr[], int n) {
for(int i=0; i<n-1; ++i) { // 准备装逼n-1次
int min_idx = i; // 先假装自己最牛逼
for(int j=i+1; j<n; ++j) { // 挨个瞅后面小弟
if(arr[j] < arr[min_idx]) { // 发现更菜的
min_idx = j; // 立马换人
}
}
swap(arr[i], arr[min_idx]); // 把最菜的拎到前面
}
}
int main()
{
int arr[10] = {5, 2, 3, 1, 7, 4, 9, 0, 8, 6};
selectionSort(arr, 10);
for(int i:arr) cout << i << " ";
//0 1 2 3 4 5 6 7 8 9
return 0;
}
Python版：
def selection_sort(arr):
n = len(arr)
for i in range(n-1): # 装逼次数
min_idx = i # 先自封老大
for j in range(i+1, n): # 后面小弟排队
if arr[j] < arr[min_idx]: # 发现更菜的
min_idx = j # 换老大
arr[i], arr[min_idx] = arr[min_idx], arr[i] # 新老大上位
arr = [5, 2, 3, 1, 7, 4, 9, 0, 8, 6]
selection_sort(arr)
print(arr)
#[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
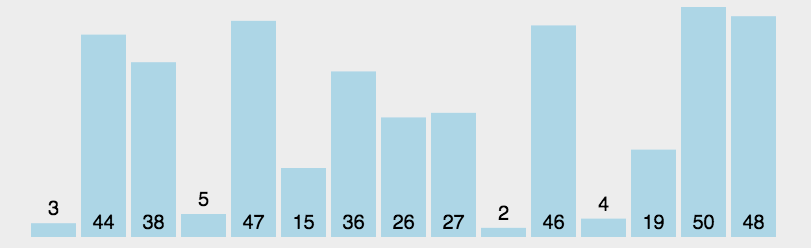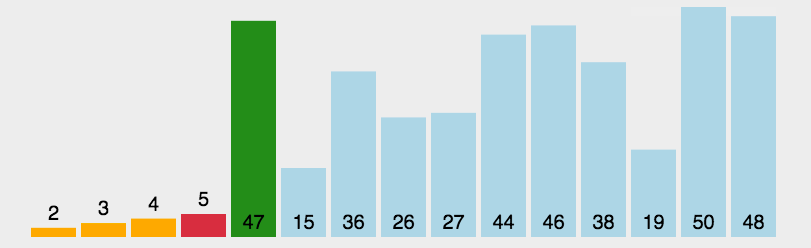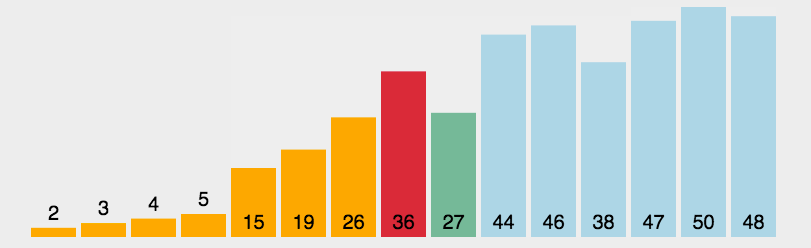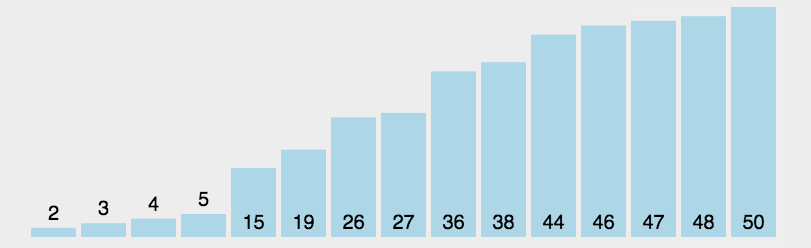
3. 插入排序（跟打扑克摸牌一样）
这操作就跟打麻将摸牌似的，摸一张插到合适的位置！
思路
（1）每次挑一个最小的，放好。
（2）在剩下的里面挑一个再放好。
C++版：
#include <bits/stdc++.h>
using namespace std;
void insertionSort(int arr[], int n) {
for(int i=1; i<n; ++i) { // 从第二张牌开始装逼
int key = arr[i]; // 新摸的牌
int j = i-1; // 从最后一张开始比
while(j>=0 && arr[j]>key) { // 前面的牌都特么太大
arr[j+1] = arr[j]; // 往后挪位置
j--;
}
arr[j+1] = key; // 终于找到合适的位置
}
}
int main()
{
int arr[10] = {5, 2, 3, 1, 7, 4, 9, 0, 8, 6};
insertionSort(arr, 10);
for(int i:arr) cout << i << " ";
//0 1 2 3 4 5 6 7 8 9
return 0;
}
Python版：
def insertion_sort(arr):
for i in range(1, len(arr)): # 从第二个开始装
key = arr[i] # 新来的牌
j = i-1 # 准备跟前任们比大小
while j >=0 and key < arr[j]: # 前面的都是大佬
arr[j+1] = arr[j] # 大佬往后稍
j -= 1
arr[j+1] = key # 找到自己的坑
arr = [5, 2, 3, 1, 7, 4, 9, 0, 8, 6]
insertion_sort(arr)
print(arr)
#[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
4. 快速排序（分而治之的扛把子）
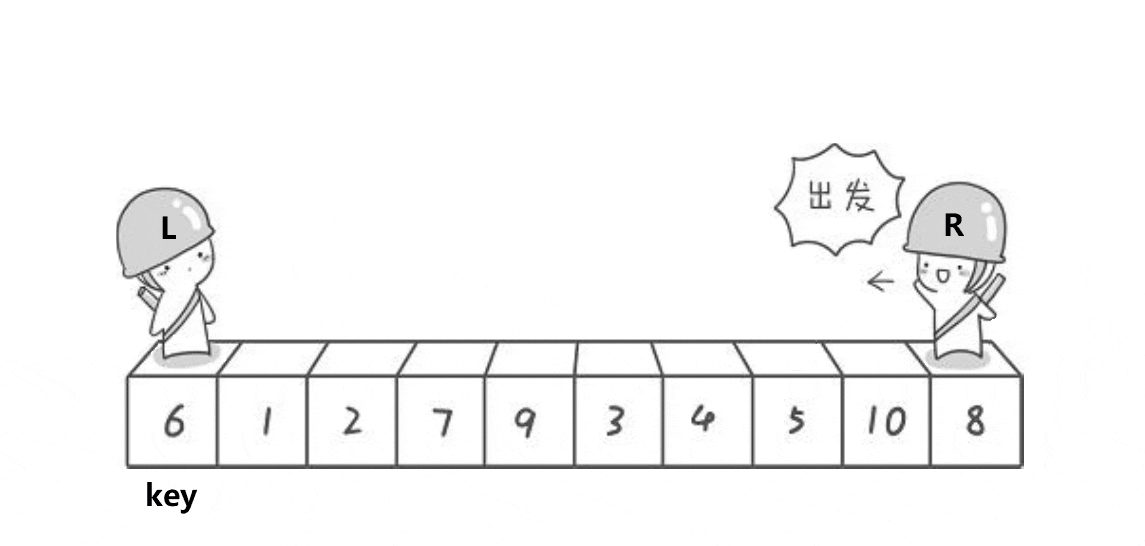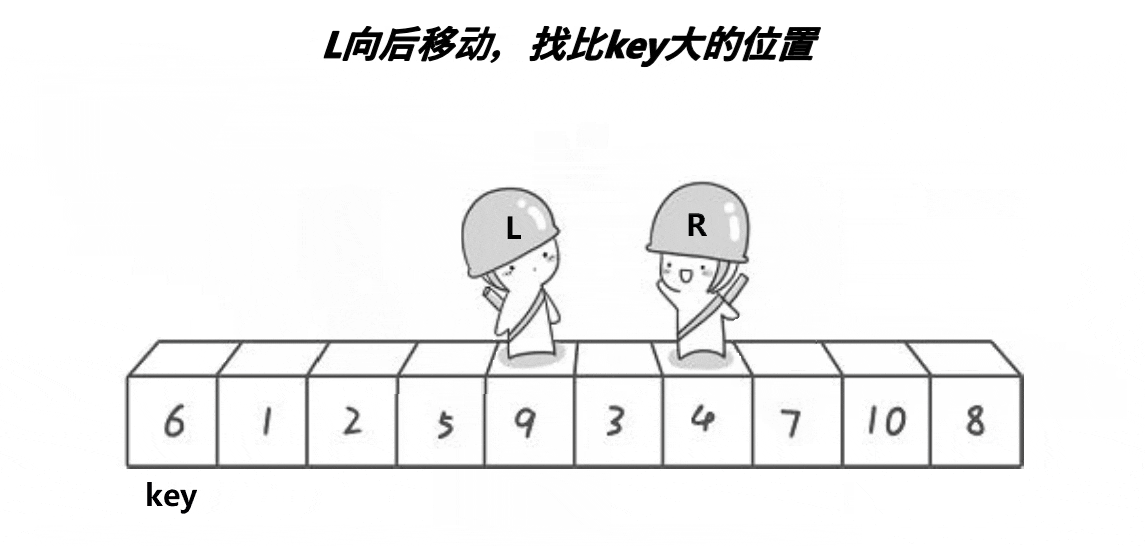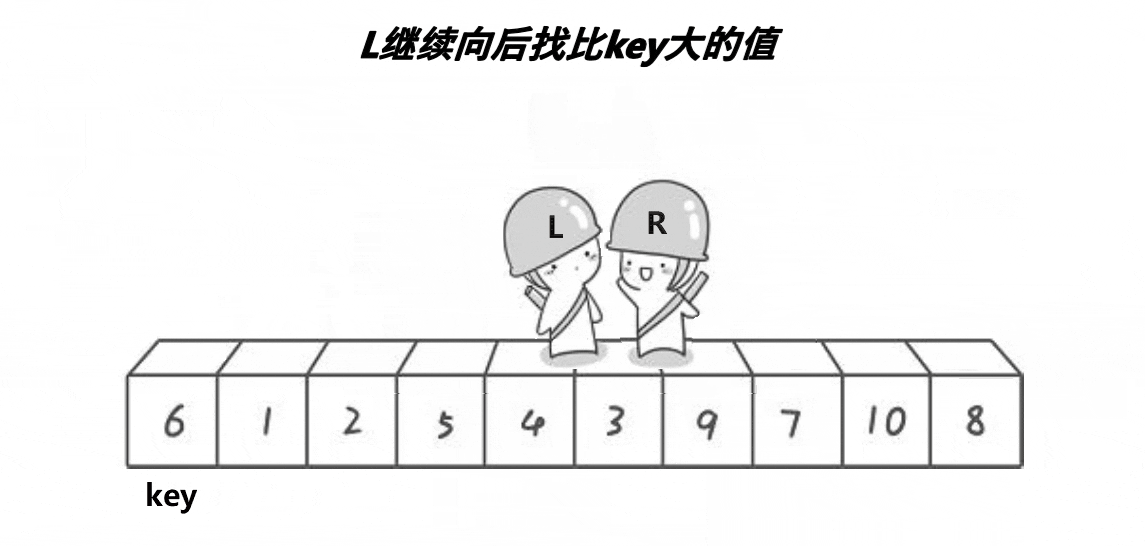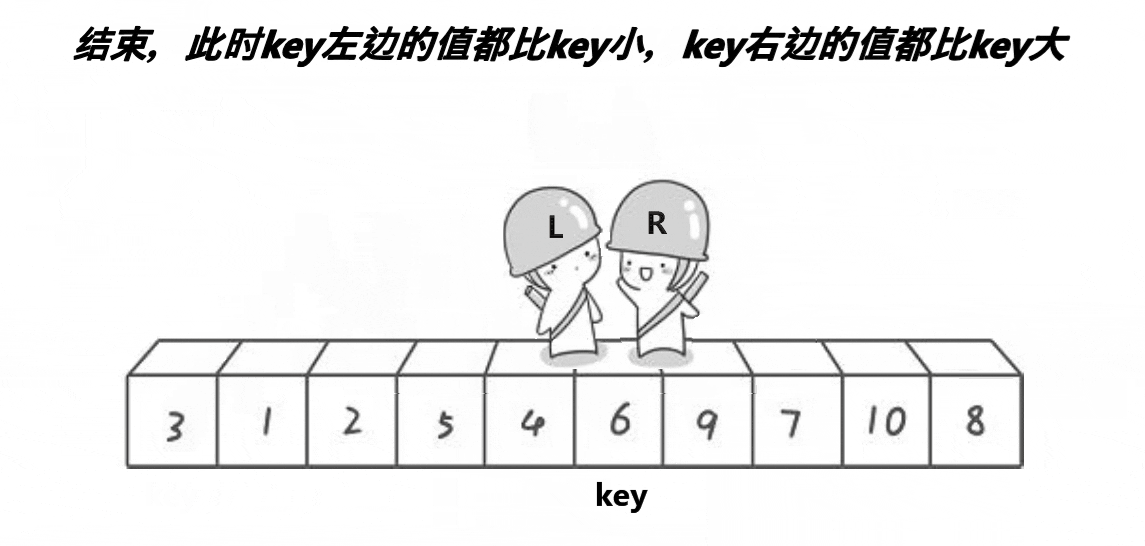
这货就跟黑社会抢地盘一样，先找个扛把子，小的站左边，大的站右边！
思路
（1）确定一个扛把子，把比它大的放右边，比它小的放左边
（2）重新确定一个扛把子，比它大的放右边，比它小的放左边
（3）重复上述操作
C++版：
#include <bits/stdc++.h>
using namespace std;
int partition(int arr[], int low, int high) {
int pivot = arr[high]; // 选最后一个人当扛把子
int i = low - 1; // 马仔起始位置
for(int j=low; j<high; ++j) {
if(arr[j] < pivot) { // 比扛把子菜的
i++; // 马仔队伍扩张
swap(arr[i], arr[j]); // 收编小弟
}
}
swap(arr[i+1], arr[high]); // 扛把子坐正位
return i+1;
}
void quickSort(int arr[], int low, int high) {
if(low < high) {
int pi = partition(arr, low, high); // 抢地盘
quickSort(arr, low, pi-1); // 左边继续干
quickSort(arr, pi+1, high); // 右边继续干
}
}
int main()
{
int arr[10] = {5, 2, 3, 1, 7, 4, 9, 0, 8, 6};
quickSort(arr, 0, 10);
for(int i:arr) cout << i << " ";
//0 1 2 3 4 5 6 7 8 9
return 0;
}
Python版：
def quick_sort(arr):
if len(arr) <= 1: # 就剩一个还排个毛
return arr
pivot = arr[-1] # 选最后的大冤种当扛把子
left = [x for x in arr[:-1] if x < pivot] # 左边的小弟
right = [x for x in arr[:-1] if x >= pivot] # 右边的打手
return quick_sort(left) + [pivot] + quick_sort(right) # 继续干架
arr = [5, 2, 3, 1, 7, 4, 9, 0, 8, 6]
quick_sort(arr)
print(arr)
#[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
5. 归并排序（温柔的分家大师）
这货就像居委会大妈，把数组拆得稀碎再慢慢撮合！
思路
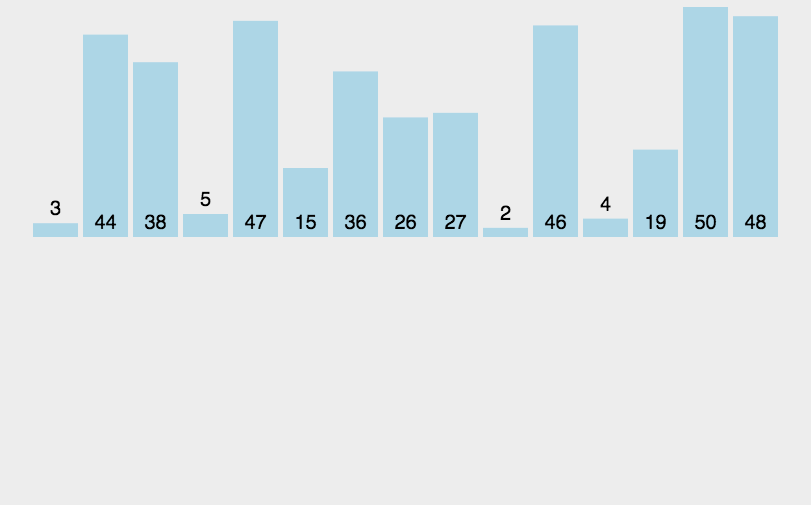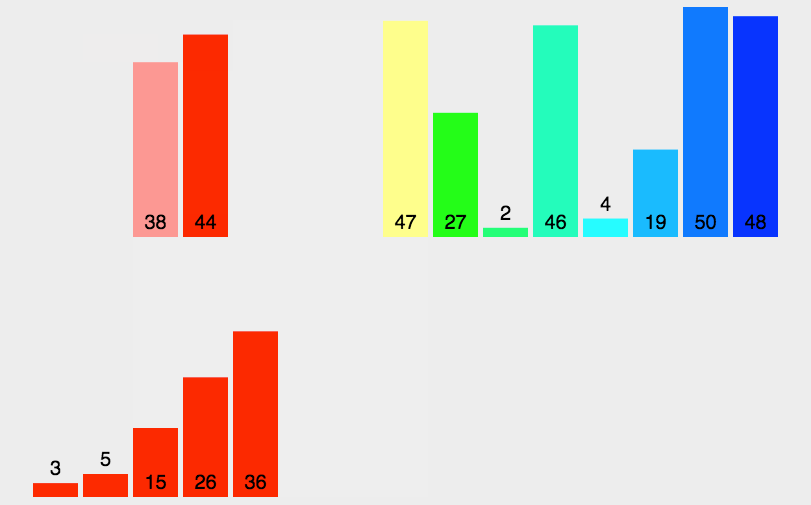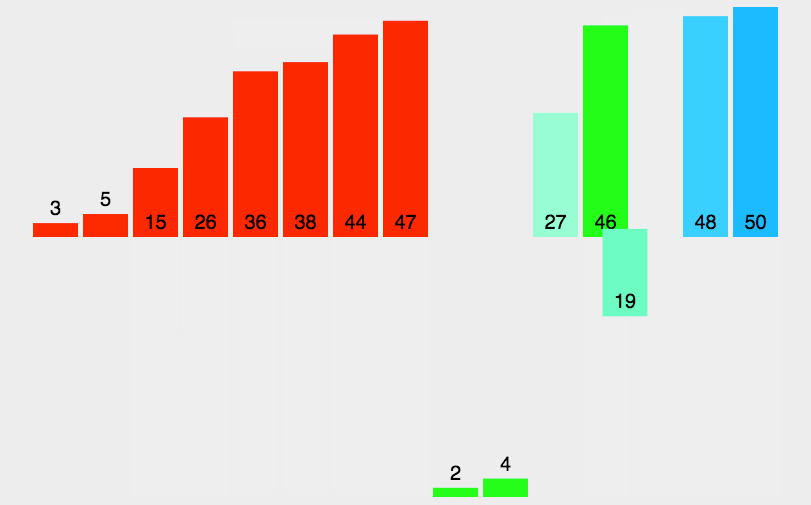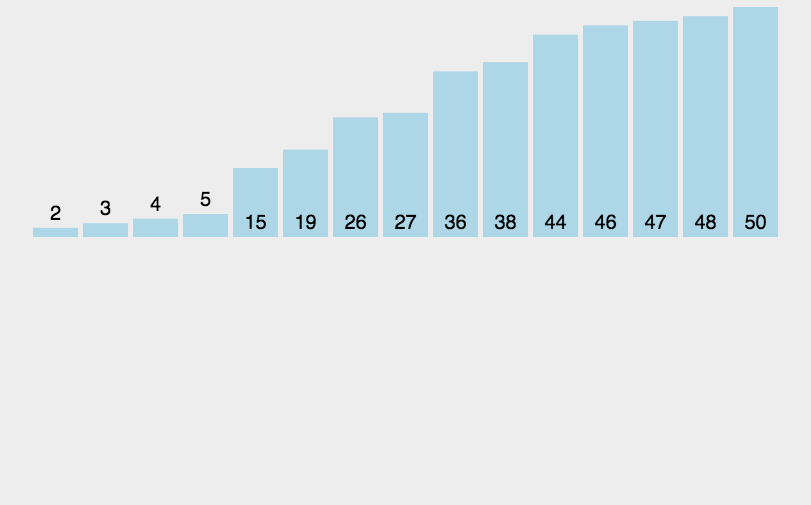
（1）将数组切分成小零碎（只有一个元素），可以认为只包含一个元素的子表是有序表。
（2）将两两合并，每合并一次，就会产生一个新的且更长的有序表。
（3）重复这一步骤，直到最后只剩下一个子表，这个子表就是排好序的线性表。
C++版：
#include <bits/stdc++.h>
using namespace std;
void merge(int arr[], int l, int m, int r) {
int n1 = m - l + 1;
int n2 = r - m;
int L[n1], R[n2];
for(int i=0; i<n1; ++i) L[i] = arr[l+i];
for(int j=0; j<n2; ++j) R[j] = arr[m+1+j];
int i=0, j=0, k=l;
while(i<n1 && j<n2) { // 左右两边比大小
if(L[i] <= R[j]) arr[k++] = L[i++];
else arr[k++] = R[j++];
}
while(i < n1) arr[k++] = L[i++]; // 收尾左边
while(j < n2) arr[k++] = R[j++]; // 收尾右边
}
void mergeSort(int arr[], int l, int r) {
if(l >= r) return;
int m = l + (r-l)/2; // 找中间点劈腿
mergeSort(arr, l, m); // 左边搞基
mergeSort(arr, m+1, r); // 右边搞基
merge(arr, l, m, r); // 合体！
}
int main()
{
int arr[10] = {5, 2, 3, 1, 7, 4, 9, 0, 8, 6};
mergeSort(arr, 0, 10);
for(int i:arr) cout << i << " ";
//0 1 2 3 4 5 6 7 8 9
return 0;
}
Python版：
def merge_sort(arr):
if len(arr) <= 1: # 拆到不能再拆
return arr
mid = len(arr) // 2 # 中间劈腿
left = merge_sort(arr[:mid]) # 左边小分队
right = merge_sort(arr[mid:]) # 右边小分队
return merge(left, right) # 合体！
def merge(left, right):
result = []
i = j = 0
while i < len(left) and j < len(right): # 两边比大小
if left[i] < right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result += left[i:] # 收尾左边
result += right[j:] # 收尾右边
return result
arr = [5, 2, 3, 1, 7, 4, 9, 0, 8, 6]
merge_sort(arr)
print(arr)
#[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
总结
每个排序都有每个排序的尿性，择优使用。
-
冒泡：简单但慢得像乌龟（O(n²)）
-
选择：永远在找最小的那个（O(n²)）
-
插入：适合小规模装逼（O(n²)）
-
快排：平均快如闪电（O(n log n)），但最差会翻车
-
归并：稳定可靠的老司机（O(n log n)），但费内存
代码留着复习：
链接：小白兔的礼物——排序算法
提取码：mcYN
感谢大伙观看，别忘了三连支持一下
大家也可以关注一下我的其它专栏，同样精彩喔~
下期见咯~
风语者！平时喜欢研究各种技术，目前在从事后端开发工作，热爱生活、热爱工作。
站长推荐
- QT多线程的5种用法，通过使用线程解决UI主界面的耗时操作代码，防止界面卡死。
QT多线程的5种用法，通过使用线程解决UI主界面的耗时操作代码，防止界面卡死。... - U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 - stm32使用HAL库配置串口中断收发数据（保姆级教程）
stm32使用HAL库配置串口中断收发数据（保姆级教程） - 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效) - Allegro16.6差分等长设置及走线总结
Allegro16.6差分等长设置及走线总结