探索图的遍历方式：深度优先遍历与宽度优先遍历网站首页 技术交流

探索图的遍历方式：深度优先遍历与宽度优先遍历

Lostgreen 2025-07-30 12:01:04

简介探索图的遍历方式：深度优先遍历与宽度优先遍历

引言

在图论中，图的遍历是一个基础而重要的问题。遍历图的过程可以理解为访问图中的每一个顶点，并确保每个顶点都被访问且仅被访问一次。深度优先遍历（Depth-First Search, DFS）和宽度优先遍历（Breadth-First Search, BFS）是两种最常用的图遍历方式。它们在解决图的连通性、路径查找、拓扑排序等问题中有着广泛的应用。本文将详细介绍这两种遍历方式的基本思想、实现方法、应用场景以及它们之间的对比。

背景知识

图的基本概念

图（Graph）：由顶点（Vertex）和边（Edge）组成的结构，可以表示为 $G = (V, E)$ ，其中 $V$ 是顶点集， $E$ 是边集。
有向图与无向图：边是否有方向性。
连通图：图中任意两个顶点之间都存在路径。
树（Tree）：一种特殊的图，具有以下性质：
- 连通且无环。
- 有 $n$ 个顶点和 $n - 1$ 条边。

遍历的意义

图的遍历是解决许多图论问题的基础，例如：

判断图的连通性。
寻找图中的路径或环。
拓扑排序。
求解最小生成树或最短路径。

深度优先遍历（DFS）

基本思想

深度优先遍历的核心思想是“一条路走到黑”。从起始顶点出发，沿着一条路径尽可能深入地访问顶点，直到无法继续为止，然后回溯到上一个顶点，继续探索其他路径。

算法步骤

初始化：选择一个起始顶点，标记为已访问。
递归探索：从当前顶点出发，访问一个未被访问的邻接顶点，并递归地进行深度优先遍历。
回溯：当当前顶点的所有邻接顶点都被访问后，回溯到上一个顶点。

伪代码

def dfs(graph, start, visited):
    visited[start] = True  # 标记当前顶点为已访问
    print(start)  # 访问当前顶点

    for neighbor in graph[start]:  # 遍历当前顶点的邻接顶点
        if not visited[neighbor]:
            dfs(graph, neighbor, visited)  # 递归访问邻接顶点

实现细节

递归实现：利用函数调用栈实现回溯。
非递归实现：使用栈模拟递归过程。

应用场景

连通性检测：判断图是否连通。
拓扑排序：用于有向无环图（DAG）的拓扑排序。
寻找路径：查找两个顶点之间的路径。

宽度优先遍历（BFS）

基本思想

宽度优先遍历的核心思想是“逐层扩展”。从起始顶点出发，先访问其所有邻接顶点，然后再依次访问这些邻接顶点的邻接顶点，直到所有顶点都被访问。

算法步骤

初始化：选择一个起始顶点，标记为已访问，并将其加入队列。
逐层访问：从队列中取出一个顶点，访问其所有未被访问的邻接顶点，并将它们加入队列。
重复：重复步骤2，直到队列为空。

伪代码

from collections import deque

def bfs(graph, start):
    visited = [False] * len(graph)  # 初始化访问标记
    queue = deque([start])  # 初始化队列
    visited[start] = True  # 标记起始顶点为已访问

    while queue:
        vertex = queue.popleft()  # 取出队列中的顶点
        print(vertex)  # 访问当前顶点

        for neighbor in graph[vertex]:  # 遍历当前顶点的邻接顶点
            if not visited[neighbor]:
                visited[neighbor] = True  # 标记邻接顶点为已访问
                queue.append(neighbor)  # 将邻接顶点加入队列

实现细节

队列的使用：利用队列的先进先出（FIFO）特性实现逐层访问。

应用场景

最短路径：在无权图中求解最短路径。
连通性检测：判断图是否连通。
层级遍历：按层级访问树或图的顶点。

DFS与BFS的对比

1. 遍历顺序

DFS：沿着一条路径尽可能深入地访问顶点，直到无法继续为止，然后回溯。
BFS：逐层访问顶点，先访问离起始顶点最近的顶点。

2. 数据结构

DFS：使用栈（递归调用栈或显式栈）。
BFS：使用队列。

3. 时间复杂度

DFS： $O (V + E)$ ，其中 $V$ 是顶点数， $E$ 是边数。
BFS： $O (V + E)$ ，与DFS相同。

4. 空间复杂度

DFS：取决于递归深度，最坏情况下为 $O (V)$ 。
BFS：取决于队列大小，最坏情况下为 $O (V)$ 。

5. 适用场景

DFS：适合寻找路径、拓扑排序、连通性检测等问题。
BFS：适合求解最短路径、层级遍历等问题。

代码实现

DFS的实现

ACWing 树的重心

给定一棵树，树中包含 $n$ 个结点（编号 $1 \sim n$ ）和 $n - 1$ 条无向边。要求找到树的重心，并输出将重心删除后，剩余各个连通块中点数的最大值。

重心定义：重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。

输入格式

第一行包含整数 $n$ ，表示树的结点数。
接下来 $n - 1$ 行，每行包含两个整数 $a$ 和 $b$ ，表示点 $a$ 和点 $b$ 之间存在一条边。

输出格式

输出一个整数 $m$ ，表示将重心删除后，剩余各个连通块中点数的最大值。

解题思路

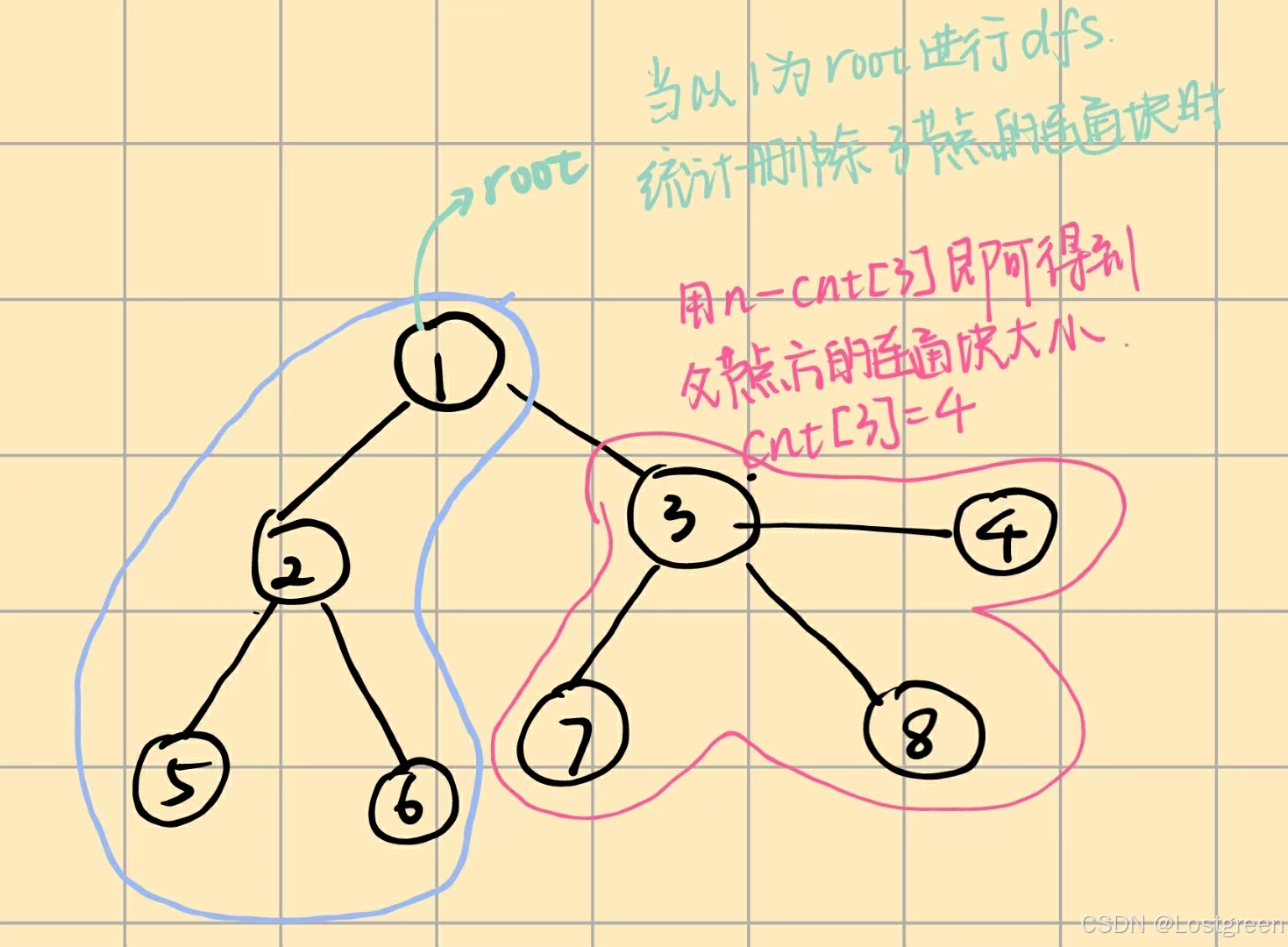
我们可以通过深度优先搜索（DFS）遍历树，计算每个结点作为重心时的最大连通块大小，最终选择最小的最大值对应的结点作为重心。

具体步骤如下：

DFS遍历：从任意一个结点（如根结点）开始，递归遍历树的每个结点。
计算子树大小：对于每个结点，计算其子树的大小，并记录删除该结点后，剩余连通块的最大值。
更新重心：在遍历过程中，记录最小的最大值对应的结点。

关键代码:对于非子节点的连通块，可以用总节点数减去当前连通块个数来实现计算。

在这里插入图片描述

3. 代码实现

以下是基于DFS的树的重心问题的代码实现：

#include <iostream>
#include <cstring>
using namespace std;

const int MAX_NODES = 2e5 + 7; // 定义最大节点数

// 邻接表存储树的相关数组
int head[MAX_NODES], targetNode[MAX_NODES], nextEdge[MAX_NODES], edgeIndex = 0;
// cnt[node] 表示以 node 为根的子树大小
// blockSize[node] 表示删除 node 后的最大连通块大小
int subtreeSize[MAX_NODES], blockSize[MAX_NODES];
int nodeCount; // 树的节点数

/**
 * 添加一条无向边到邻接表中
 * @param fromNode 起始节点
 * @param toNode 目标节点
 */
void addEdge(int fromNode, int toNode) {
    nextEdge[++edgeIndex] = head[fromNode];
    head[fromNode] = edgeIndex;
    targetNode[edgeIndex] = toNode;
}

/**
 * 深度优先搜索（DFS）遍历树，计算每个节点的子树大小和删除该节点后最大的连通块大小
 * @param currentNode 当前处理的节点
 * @param parent 当前节点的父节点
 * @return 返回以当前节点为根的子树大小
 */
int depthFirstSearch(int currentNode, int parent) {
    for (int i = head[currentNode]; i != -1; i = nextEdge[i]) {
        int childNode = targetNode[i];
        if (childNode == parent) continue; // 避免重复访问父节点

        int childSubtreeSize = depthFirstSearch(childNode, currentNode); // 递归计算子树大小
        blockSize[currentNode] = max(blockSize[currentNode], childSubtreeSize); // 更新删除当前节点后的最大连通块大小
        subtreeSize[currentNode] += childSubtreeSize; // 累加子树大小
    }

    subtreeSize[currentNode] += 1; // 包括当前节点本身
    blockSize[currentNode] = max(blockSize[currentNode], nodeCount - subtreeSize[currentNode]); // 更新删除当前节点后的最大连通块大小
    return subtreeSize[currentNode]; // 返回以当前节点为根的子树大小
}

int main() {
    ios::sync_with_stdio(false); // 提高I/O效率
    cin.tie(0);
    cout.tie(0);

    cin >> nodeCount;
    memset(head, -1, sizeof head); // 初始化邻接表

    // 输入 n-1 条边，构建无向图
    for (int i = 1; i < nodeCount; ++i) {
        int nodeX, nodeY;
        cin >> nodeX >> nodeY;
        addEdge(nodeX, nodeY); // 添加无向边
        addEdge(nodeY, nodeX);
    }

    depthFirstSearch(1, -1); // 从节点 1 开始 DFS

    int minBlockSize = 1e6; // 初始化最小最大连通块大小
    for (int i = 1; i <= nodeCount; ++i) {
        if (blockSize[i] < minBlockSize) {
            minBlockSize = blockSize[i]; // 更新最小最大连通块大小
        }
    }

    cout << minBlockSize << endl; // 输出结果
    return 0;
}

BFS的实现

ACWing 图中节点的层次

#include <iostream>
#include <queue>
#include <cstring>
using namespace std;

const int MAX_NODES = 1e5 + 7; // 定义最大节点数

// 邻接表相关变量
int head[MAX_NODES], targetNode[MAX_NODES], nextEdge[MAX_NODES], edgeIndex = 0;
// 距离数组，初始化为一个很大的值表示无穷大
int distanceToNode[MAX_NODES];

/**
 * 添加边到邻接表中
 * @param fromNode 起始节点
 * @param toNode 目标节点
 */
void addEdge(int fromNode, int toNode) {
    // 将新边插入链表头部
    nextEdge[++edgeIndex] = head[fromNode];
    head[fromNode] = edgeIndex;
    targetNode[edgeIndex] = toNode;
}

/**
 * 使用广度优先搜索计算从起点到终点的最短路径长度
 * @param startNode 起点
 * @param endNode 终点
 */
void breadthFirstSearch(int startNode, int endNode) {
    // 初始化所有节点的距离为无穷大
    memset(distanceToNode, 0x3f, sizeof distanceToNode);
    queue<int> nodeQueue;
    distanceToNode[startNode] = 0; // 起点到自身的距离为0
    nodeQueue.push(startNode);

    while (!nodeQueue.empty()) {
        int currentNode = nodeQueue.front();
        nodeQueue.pop();

        // 遍历当前节点的所有邻接节点
        for (int i = head[currentNode]; i != -1; i = nextEdge[i]) {
            if (distanceToNode[targetNode[i]] == 0x3f3f3f3f) { // 如果该节点尚未访问过
                distanceToNode[targetNode[i]] = distanceToNode[currentNode] + 1; // 更新距离
                nodeQueue.push(targetNode[i]); // 将该节点加入队列
            }
        }
    }

    // 输出结果：如果终点不可达，则输出-1；否则输出到达终点的最短距离
    if (distanceToNode[endNode] == 0x3f3f3f3f)
        cout << -1 << endl;
    else
        cout << distanceToNode[endNode] << endl;
}

int main() {
    ios::sync_with_stdio(false); // 提高I/O效率
    cin.tie(0);
    cout.tie(0);

    int nodeCount, edgeCount;
    cin >> nodeCount >> edgeCount;
    memset(head, -1, sizeof head); // 初始化head数组为-1，表示没有边

    // 输入每条边的信息，并调用addEdge函数将其添加到邻接表中
    for (int i = 1; i <= edgeCount; ++i) {
        int fromNode, toNode;
        cin >> fromNode >> toNode;
        addEdge(fromNode, toNode);
    }

    // 执行BFS算法，从节点1开始寻找到达最后一个节点的最短路径
    breadthFirstSearch(1, nodeCount);

    return 0;
}